Метод бинарных элементов в задачах динамики разрушения горных пород

В задачах динамики разрушения всегда существует проблема выбора эффективного метода численного моделирования и выбора модели разрушения. Сложные пространственные конечные элементы, наиболее точно описывающие упругое и упруго-пластичное поведение среды, становится громоздкими и неэффективными в задачах разрушения.

Перед нами стояла задача создания простого и скоростного метода трёхмерного моделирования динамических процессов при произвольно заданной нагрузке, с простой и понятной моделью разрушения.

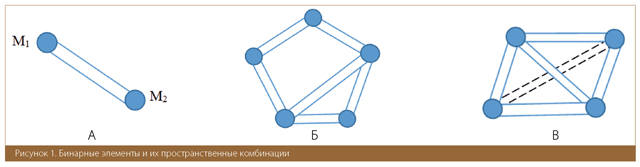
Представим произвольное тело в виде набора сосредоточенных масс, соединённых между собой линейными связями. Таким образом в качестве базового элемента мы принимаем систему в виде цилиндра с двумя массами на концах (рис. 1А). Такую конструкцию назовём бинарным элементом.

Распределение масс по пространству выполняется в соответствии с плотностью среды таким образом, чтобы сохранялся закон сохранения массы. Пространственная картина выглядит в виде сетки из бинарных элементов, соединённых в узлах. Массы соседних элементов объединяются в узлах простым сложением (рис. 1Б).

Для простоты сетка бинарных элементов строится на основе тетраэдральной сетки как наиболее распространённой и наиболее точно описывающей любое произвольное тело. За основу для создания системы бинарных элементов взят тетраэдр (рис. 1В).

Узловые массы определены как масса тетраэдра, поделённая на четыре. А объём бинарного элемента как объём тетраэдра, поделённый на шесть. Объёмы и массы при присоединении смежных тетраэдров объединяются простым сложением.

В результате получаем пространственную сетку бинарных элементов, наделённых стандартными физико-механическими свойствами (модуль Юнга, коэффициент Пуассона, плотность, пределы прочности на растяжении, сжатие и сдвиг).

Динамика процесса и схема интегрирования по времени приводятся с применением явной схемы, что позволяет отказаться от громоздкой матрицы жёсткости и тем самым на порядки сократить время расчётов.

Явный метод подразумевает, что заданный интервал времени делится на отрезки времени — шаги. Основываясь на состоянии системы на предыдущем шаге и зная, какие нагрузки приложены текущем шаге, можно, используя известные методы интегрирования по времени (конечно-разностную схему или метод Ньюмарка), определить ускорение, скорость и смещение.

Затем, используя метод приращений, по определённым перемещениям вычисляем деформации и напряжения в каждом элементе. Полученные напряжения анализируем, применяя модель разрушения. Для простоты мы использовали упруго-хрупкую модель.

Если растягивающие напряжения превышают предел прочности на растяжение, то напряжении в таком элементе обнуляются.

Фиксируется признак разрушения такого элемента, и в дальнейшем он уже не может нести растягивающую нагрузку. Но продолжает нести сжимающую, если трещина схлопывается. Если сжимающие напряжения в элементе превышают предел прочности на сжатие, то фиксируется такой признак разрушения, и элемент не передает сжимающую нагрузку, превышающую предел прочности на сжатие.

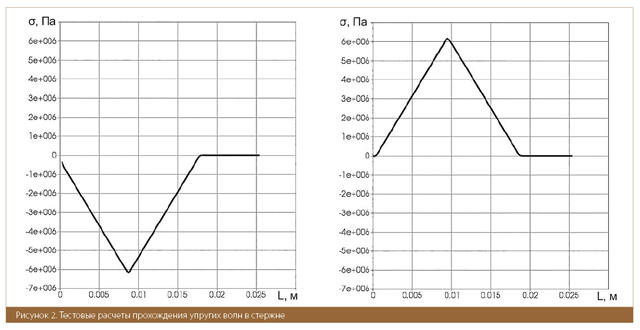
Для проверки устойчивости динамической системы были проведены тестовые расчёты прохождения упругих волн в стержне, нагруженном на одном конце треугольным импульсом (Рис.2).

Неизменная форма импульса сжатия и растяжения при многократных отражениях от конца стержня свидетельствует об устойчивости динамического процесса и верном определении необходимого временного шага.

Мы провели тестовый расчет разрушения бетонной плиты при кумулятивном взрыве на его поверхности. Экспериментальные данные были взяты из известной статьи [1]. Данный эксперимент взят за основу для тестирования в работах практически всех разработчиков программ моделирования разрушения при динамических нагрузках.

Характеристики материала:

• модуль Юнга: E=2.1581010 H/м²;
• коэффициент Пуассона: v=0.3;
• плотность: ρ=2.75кг/м³;
• предел прочности на растяжение: σp=3.984106 H/м²;
• предел прочности на сжатие: σст=4.8107 H/м²;
• предел прочности на сдвиг: σсд=8.64*106 H/м².

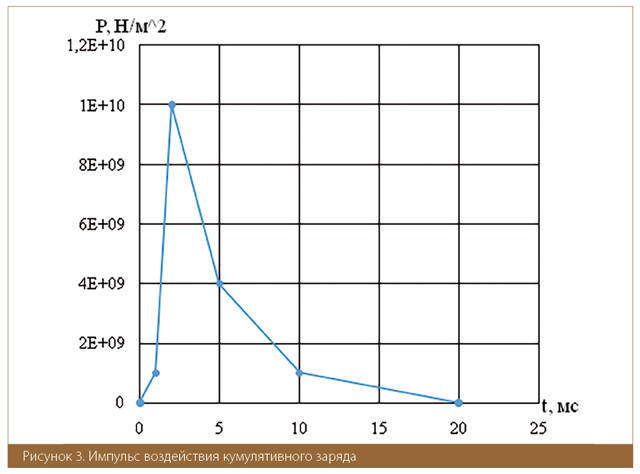
Воздействие кумулятивного заряда представлено на рис. 3.
Заметим, что мы решили действительную трёхмерную задачу, в то время как многие авторы используют лишь плоскую осесимметричную задачу.

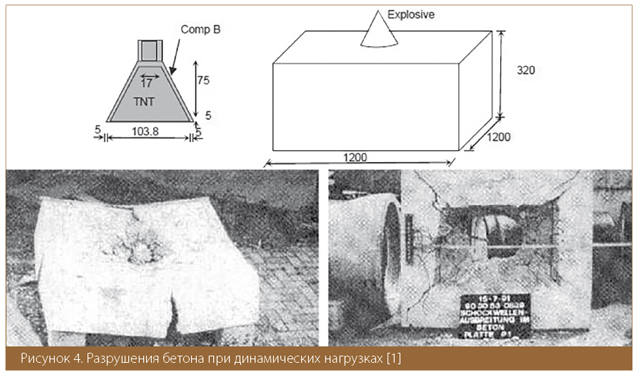
Хорошие результаты сравнения с экспериментом дают основание использования метода бинарных элементов в практических задачах определения зон разрушения при взрывной нагрузке (рис.5).

В качестве примеров использования метода бинарных элементов были проведены расчёты зон разрушения на уступе карьера скважинным зарядом в различных вариантах. Одиночная скважина, две скважины с одновременной детонацией, либо с задержкой (рис.6).

Кроме определённых зон разрушения, метод позволяет получить полный набор динамических характеристик среды в произвольной точке и в произвольный момент времени (поля ускорений, скоростей, смещений, детальную картину напряжено деформированного состояния).

Полученные данные о векторах движения масс могут послужить основой для баллистических расчётов разлёта разрушенной породы и построении развала.

Список литературы

1. Rabczuk T. and Eibl J. Modelling dynamic failure of concrete with mesh free methods. International Journal of Impact Engineering, 32: 1878–1897, 2006.

Текст: В. В. Григорьев, Институт коммуникаций и информационных технологий Кыргызско-Российского Славянского университета

ОсОО «Blast Maker»
720000, Кыргызская Республика, Бишкек, ул. Киевская, 44
тел.: +996 (312) 66-01-40
blastmaker@istc.kg www.blastmaker.kg