Нашли ошибку? Выделите ее мышкой
и нажмите Ctrl + Enter

Инварианты физических параметров разрушения неоднородных горных пород и массива при действии объёмного напряжённого состояния

Главная / Горная промышленность / Инварианты физических параметров разрушения неоднородных горных пород и массива при действии объёмного напряжённого состояния

19.05.2017

В начале аналитического исследования, выполняемого в настоящем сообщении, является применение научных положений общей теории напряжённого и деформированного состояния в материале сплошной среды [1].

Затем, при построении и использовании математических моделей инвариантов главных напряжений и главных деформаций [1], выполняются дополнительные включения математических соотношений для описания изменения механического состояния массива и обоснования механической модели энергетического критерия прочности неоднородных горных пород.

Логически целесообразным этапом научного исследования является обоснование параметров напряжённого и деформированного состояния сплошной среды (в частности массива горных пород) и установление механических свойств материала при действии объёмного напряжённого состояния и составление на их основе уравнений получения физических и механических показателей механического состояния, деформируемых твёрдых тел.

Механический процесс перераспределения объёмного напряжённого состояния протекает в зоне максимальных сжимающих напряжений и в зоне предельных состояний достаточно закономерно, поэтому целесообразно дать пояснение протеканию механических стадий при различных соотношениях между главными напряжениями в основных видах объёмных напряженных состояний.

На рисунке 1 представлено распределение объёмного напряжённого состояния в виде главных напряжений σ₁, σ₂, σ₃ и изменение величины параметры Надаи [2], характеризующего различные виды объёмных напряжённых состояний.

При проведении горных выработок массив горных пород располагается в первой зоне объёмного напряжённого состояния. Обычно эта зона классифицируется в механике горных пород как зона геостатического сжатия, где формируется объёмное напряжённое состояние с соотношениями между главными напряжениями вида $\sigma_1 = \sigma_2 \ge \sigma_3$

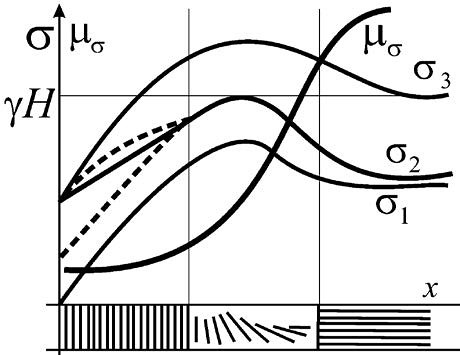
Рис. 1 Характер изменения трёх главных напряжений и параметра Надаи в пласте полезного ископаемого в массиве впереди очистного забоя.

Согласно теории Надаи этот вид объёмного напряжённого состояния относится к обобщённому сжатию, так как μ_G = +1 .Во второй допредельной зоне главные напряжения постепенно достигают своих максимальных сжимающих значений. При этом максимальное сжимающее напряжение σ₃ достигает своего максимального значения наиболее интенсивно, а минимальное сжимающее напряжение σ₁ возрастает значительно медленнее (рис. 1). Промежуточное главное напряжение σ₂, принимает значение, примерно равное: $\sigma_2 = \frac{1}{2(\sigma_1 + \sigma_3)}$

При значениях трех главных напряжений σ₁, $\sigma_2 = \frac{1}{2(\sigma_1 + \sigma_3)}$ , σ₃, величина параметра Надаи вычисляется по формуле (6)
и принимает значение равное нулю. Этот вид объёмного напряжённого состояния относится к обобщённому сдвигу, так как μ_G = 0.

Третья зона горных пород массива вблизи горной выработки для достаточно нарушенных горных пород характеризуется физическим состоянием доразрушения, в которой, вследствие влияния выработки, могут сформировываться трещины похожие по форме существующей выработки впереди забоя, а три главных напряжения теряют свою способность к сопротивлению действующим нагрузкам по всем трём направлениям воздействия.

В этой зоне величина максимального сжимающего напряжения уменьшается до величины промежуточного главного напряжения, а величина главного минимального сжимающего напряжения стремится к нулю. В этой зоне нагружения формируется объёмное напряжённое состояние со следующими соотношениями между главными напряжениями σ₃ = σ₂; σ₁ ≈ 0.

Этот вид объёмного напряжённого состояния относится к обобщённому растяжению, так как μ_G = -1. В этой зоне реализуется значительная величина максимальной растягивающей деформации ε₁.

Исследования по выбору и определению главных напряжений объёмного напряжённого состояния и параметров изменения механического состояния породного массива в математических моделях деформируемых твёрдых тел осуществляются следующим образом [3,4].

Вначале выбираются исходные данные компонентов полного поля напряжений при действии объёмного напряжённого состояния и компоненты полного поля деформаций при действии объёмного деформированного состояния.

Компоненты тензора напряжений состоят из девяти напряжений объёмного напряжённого состояния, действующего по трём взаимно перпендикулярным осям координат х, y, z, и, кроме того, комбинация касательных напряжений в этом тензоре напряжений является симметричной относительно главной диагонали тензора осевых напряжений.

Написание тензора напряжений для объёмного напряжённого состояния среды представляется следующим образом (1):

T_G = \begin {bmatrix}\sigma_x\tau_{xy}\tau_{xz}\\ \tau_{yx}\sigma_y\tau_{yz}\\ \tau_{zx}\tau_{zy}\sigma_{z}\end{bmatrix}

где T_G — тензор компонент напряжений объёмного напряжённого состояния массива горных пород. При этом

\tau_{xy} = \tau_{yx},\tau_{xz} = \tau_{zx}, \tau_{yz} = \tau_{zy}

Таким же образом составляется тензор деформаций для соответствующего поля деформаций. Из переменных компонент объёмного напряжённого состояния, записанного в тензоре (1) для поля напряжений, составляется математическая модель определения компонент главных напряжений σ₁, σ₂, σ₃ расположенных в главных координатных осях, а математические операции состоят из следующих действий. Выбирается так называемый шаровой тензор из компонент искомых величин объёмного напряжённого состояния σ в тензоре (2):

T_{SCH} =\begin {bmatrix}\sigma 00\\ 0\sigma0\\00\sigma\end{bmatrix}

Затем составляется система алгебраических уравнений, левая часть которых представляет собой разность между компонентами тензора напряжений объёмного напряжённого состояния (1) и компонентами шарового тензора (2). Правая часть этой системы уравнений представляется в виде нулевого вектора третьего порядка.

Эта система уравнений служит для определения величин тензора главных напряжений, у которого отличными от нуля являются только компоненты напряжений по главной диагонали. Раскрывая определитель третьего порядка, составленный для этой системы тензорных уравнений (3):

\begin{vmatrix} \sigma_x-\sigma\tau_{xy}\tau_{xz}\\ \tau_{yx}\sigma_{y}-\sigma\tau_{yz} \\ \tau_{zx}\tau_{zy}\sigma_{z}-\sigma\end{vmatrix}=0

получаем уравнение относительно переменной третьей степени искомого напряжения σ (4):

\sigma^{3}-\sigma^{2}(\sigma_x+\sigma_y +\sigma_z)+\sigma(\sigma_x\sigma_y+\sigma_y\sigma_z+\sigma_z\sigma_x-\tau^2_{xy}-\tau^2_{yz}-\tau^2_{zx}) - (\sigma_x \sigma_y\sigma_z+2\tau_{xy}\tau_{yz}\tau_{zx}-\sigma_x\tau^2_{yz} -\sigma_y\tau^2_{zx}-\sigma_z\tau^2_{xy})= 0

Корни уравнения (4) σ₁, σ₂, σ₃ вляются главными напряжениями, не зависят от положения осей координат, а поэтому и параметры I₁ I₂ I₃. форме инвариантов, которые не зависят от осей координат, а определяются соотношениями главных напряжений в формулах (5) равны выражениям:

I_1 = \sigma_1 + \sigma_2 + \sigma_3

I_2 = \sigma_1\sigma_2 + \sigma_2\sigma_3 + \sigma_1\sigma_3

I_3 = \sigma_1\sigma_2\sigma_3

Три взаимно перпендикулярных направления осей координат образуют главные плоскости, на которых располагаются экстремальные значения главных напряжений. Эти напряжения являются нормальными, а компоненты величин касательных напряжений

\tau_{xy} = \tau_{yz} = \tau_{xz} = 0

, равны нулю. По таким же математическим операциям согласно общей теории напряжённого и деформированного состояния в элементе сплошной среды составляются инварианты для главных деформаций(6):

\Delta_1 = \epsilon_1 + \epsilon_2 + \epsilon_3

\Delta_2 = \epsilon_1\epsilon_2 + \epsilon_2\epsilon_3 + \epsilon_3\epsilon_1

\Delta_1 = \epsilon_1 \epsilon_2 \epsilon_3

Представленные три инварианта напряжений и три инварианта деформаций могут не отражать всех возможностей комбинаций из компонентов напряжений и компонентов из деформаций, которые также инвариантны к ортогональному преобразованию координат, если включают три главных напряжения или три главных деформации в форме однородных функций.

При реализации фиксирования деформаций, характеризующих механическое состояние деформируемого твердого тела в рамках общей теории напряженного и деформированного состояния на элементарной площадке тела, зависимости между компонентами тензора главных напряжений и тензора главных деформаций определяются заданием трёх уравнений состояния, выражающих три инварианта тензора главных напряжений и три инварианта тензора главных деформаций.

Аналитические исследования, выполненные Фроммом [6], добавляют в механическую модель среды соотношения вторых и третьих инвариантов главных напряжений и деформаций в форме отношений третьего и второго инвариантов главных напряжений и второго и третьего главных деформаций.

\overline{\mu} = \frac{I^\prime_3}{(2I^\prime_2)^{\frac{2}{3}}} ;

I^\prime_2 = \frac{1}{6} \times \left[ (\sigma_1-\sigma_2)^2 + (\sigma_2 - \sigma_3)^2 + (\sigma_1 - \sigma_3)^2 \right] ;

I^\prime_3 = \frac{1}{27} \times \left[(2\sigma_1-\sigma_2-\sigma_3)\times(2\sigma_2-\sigma_3-\sigma_1)\times(2\sigma_3-\sigma_1-\sigma_2)\right] ;

\Psi^\prime_2 = \frac{1}{6} \left[ (\epsilon_1-\epsilon_2)^2 + (\epsilon_2-\epsilon_3)^2 +(\epsilon_3 - \epsilon_1)^2 \right]

\Psi^\prime_3 = \frac{1}{27}\left[(2\epsilon_1-\epsilon_2-\epsilon_3)\times(2\epsilon_2-\epsilon_3-\epsilon_1)\times(2\epsilon_3-\epsilon_1\epsilon_2) \right]

\overline{\Delta} = \frac{\Psi^\prime_3}{(2\Psi^\prime_2)^{\frac{3}{2}}} (7)

Формулы (7) определяют форму тензоров для третьих инвариантов главных напряжений и главных деформаций и позволяют установить критерий подобия тензоров главных напряжений и главных деформаций в виде следующего равенства соотношений параметров Надаи для величин главных напряжений и главных деформаций в виде следующего равенства(8): $\overline{\mu} = \overline{\Delta}$

Это равенство представляет собой математическую модель критерия подобия.

Заключение

В статье излагается аналитическая схема определения нового комплекса параметров, определяющих изменение механического состояния породного массива вблизи горных выработок. Включение в полученный комплекс дополнительного параметра Надаи позволяет составить новые математические модели механического состояния массива и энергетического критерия прочности согласно разработкам Мора [5], Надаи [2], с учетом неоднородных свойств горных пород в объёмном напряжённом состоянии. Дополнительные соотношения третьих инвариантов, включающие октаэдрические касательные напряжения и соответствующие октаэдрические деформации, позволяют составить новые критерии прочности, учитывающие энергетические и термодинамические показатели механической модели массива.

Список литературы

1. Безухов Н. И. Основы теории упругости, пластичности и ползучести. М.: Высшая школа, 1961, 538 с.

2. Надаи А. Пластичность и разрушение твёрдых тел. Т.1, М. Мир, 1969, 648 с.

3. Норель Б. К. Изменение механической прочности угольного пласта в массве. М. Наука 1983, 127 с.

4. Норель Б. К., Боровков Ю. А. Прочность горных пород в объёмном напряжённом состоянии. 978-3-659-52217-8 LAMBERT Akademic Publishing, 2013, 102 s.

5. Mohr O. Z. VDI . 1900 , 1524.

6. Fromm H . Ing .Arch 4,436, 1933

.
Текст:
Б. К. Норель, АО «ННЦ ГП ИГД им. А.А. Скочинского»,
Ю. А. Боровков, Российский государственный геологоразведочный университет им. С. Орджоникидзе (МГРИ-РГГРУ),
В. А. Азаренко, АО «ННЦ ГП ИГД им. А.А. Скочинского»